Lineare Regression
Beschreibung
Die lineare Regression wird verwendet, um eine lineare Beziehung zwischen dem Ziel und einem oder mehreren Prädiktoren zu finden. Es gibt zwei Arten der linearen Regression - Einfache und Multiple. Es ist ein nützliches Verfahren für Prognosen/Vorhersagen.
Folgende Fragen können durch die lineare Regression beantwortet werden:
- Gibt es eine Beziehung zwischen den Variablen?
- Wie stark ist die Beziehung?
- Wie genau können wir den Effekt jeder Variablen abschätzen?
- Wie genau können wir das Ziel vorhersagen?
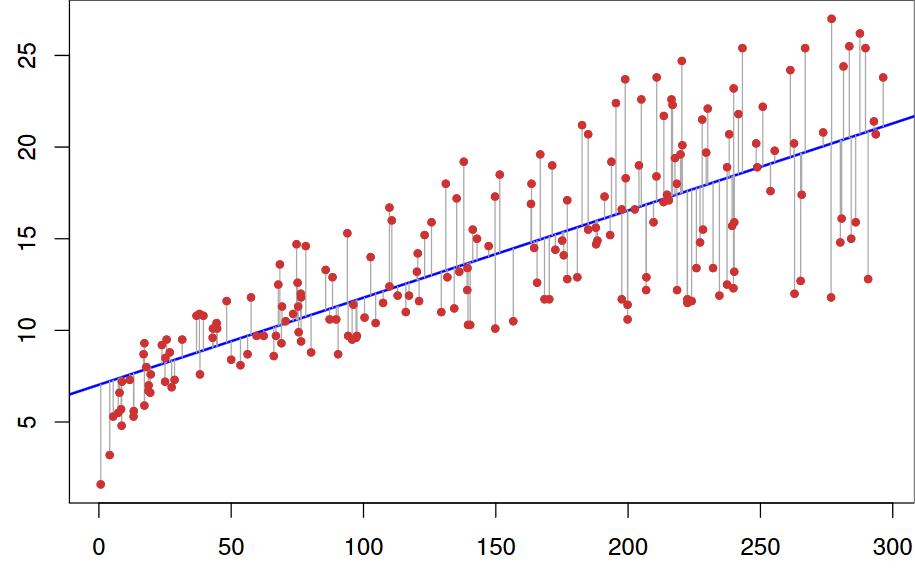
Die Kernidee ist eine Linie zu erhalten, die am besten zu den Daten passt. Die am besten geeignete Linie ist diejenige, bei der der Gesamtvorhersagefehler (alle Datenpunkte) so klein wie möglich ist. Ein Fehler ist der Abstand zwischen dem Punkt und der Regressionslinie (siehe Abbildung).
Theorie
Die einfache lineare Regression ist nützlich, um Beziehungen zwischen zwei Variablen (Prädiktor- und Ziel- bzw. unabhängige und abhängige Variable) zu finden. Jeder Datensatz wird dabei mit seinen zwei Variablen in ein Koordinatensystem eingetragen.
Da in der Realität meist mehrere Variablen ein Ziel beeinflussen, gibt es die multiple lineare Regression. Die Gleichung der multiplen linearen Regression ist der Gleichung der einfachen linearen Regression sehr ähnlich. Lediglich die Anzahl der Prädiktoren ist verschieden.
Bei der linearen Regression werden zunächst die Mittelwerte der gesamten Datenmenge berechnet. Dies erfolgt durch die Berechnung des arithmetischen Mittels:
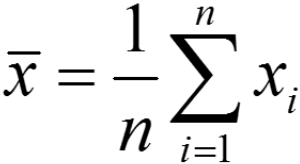
Im nächsten Schritt erfolgt das aufstellen der Regressionsgerade. Diese wird im Falle der einfachen linearen Regression definiert durch:

a: Y-Achsenabschnitt (heißt auch manchmal Intercept, Regressionskoeffizient oder slope)
b: Steigung der Regressionsgerade
Wird die multiple lineare Regression benutzt, sieht die Regressionsgleichung wie folgt aus:
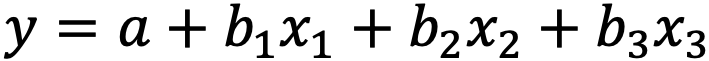
Vor- und Nachteile des Algorithmus
Vorteile:
- + Sehr leicht zu verstehen.
- + Leicht zu programmieren.
Nachteile:
- - Ungenau.
- - Ausreißer werden nicht erkannt.